1.-Definición de trigonometría y aplicaciones
2.-Reducción al primer cuadrante
3.-Radianes
4.-Teorema del seno y del coseno
5.-Ecuaciones e identidades trigonométricas
6.-Opinión/reflexión del tema
1.-Básicamente es la parte de las matemáticas que estudia las relaciones entre los lados y los ángulos de un triángulo.En términos generales es el estudio de las razones trigonométricas: seno, coseno, tangente, cotangente, secante y cosecante. Interviene directa o indirectamente en las demás ramas de las matemáticas y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión.
Hay una enorme cantidad de usos de la trigonometría y las funciones trigonométricas. Por ejemplo, la técnica de la triangulación se utiliza en astronomía para medir la distancia a las estrellas cercanas, en geografía para medir distancias entre puntos de referencia, y en los sistemas de navegación por satélite
Los campos en los que la trigonometría es necesaria son la astronomía (sobre todo para la localización de las posiciones aparentes de los objetos celestes, en los que la trigonometría esférica es esencial) y por lo tanto la navegación (en los océanos, en los aviones, y en el espacio), teoría de la música , la acústica , la óptica , el análisis de los mercados financieros, la electrónica , estadística , biología , farmacia , química , teoría de números (y por lo tanto la criptografía), sismología , meteorología , oceanografía , muchas de las ciencias físicas , la arquitectura , economía , ingeniería eléctrica , ingeniería mecánica e ingeniería civil.
2.-Se debe saber antes que nada qué son los ángulos complementarios.Es muy simple,son los que suman 180º. Si el valor de un ángulo es "A", el valor del suplementario será "180º-A".La relación de las razones trigonométricas de un ángulo con las de su suplementario va a permitir reducir ángulos del segundo al primer cuadrante.Las relaciones existentes entre las razones trigonométricas de ángulos suplementarios son:
sen (180º-A) = + sen A
cos(180º-A) = - cos A
tg (180º-A) = - tg A
cos(180º-A) = - cos A
tg (180º-A) = - tg A
Pongamos un ejercicio de ejemplo:
Reducir el angulo 127º al primer cuadrante
SOLUCIÓN:
El ángulo 127º se encuentra en el segundo cuadrante. Su suplementario por lo tanto es 180º - 127º = 53º, tenemos entonces
sen 127º = sen 53º; cos 127º = - cos 53º; tg 127º = - tg 53º
3.-El radián, al igual que el grado sexagesimal, es una unidad de medida de ángulos (de hecho es la medida de ángulo plano del Sistema Internacional de Unidades). Es decir, igual que podemos medir longitudes con metros o masas con gramos también podemos medir ángulos con radianes, expresándolo en ese caso con rad. Por cierto, la aparición del radián data del último tercio del siglo XIX, y parece que el primero que lo utilizó fue James Thompson, ingeniero y físico hermano de Lord Kelvin.
Por definición es el ángulo central de una circunferencia que abarca un arco de igual longitud que el radio de la misma.Es decir, si nuestra circunferencia tiene radio R, un radián es el ángulo que abarca un arco de longitud R:
Bien, ya que sabemos qué es un radián vamos a relacionarlo con la otra unidad de medida de ángulos que conocemos: el grado sexagesimal (o simplemente grado). La equivalencia entre estas dos medidas es la siguiente:
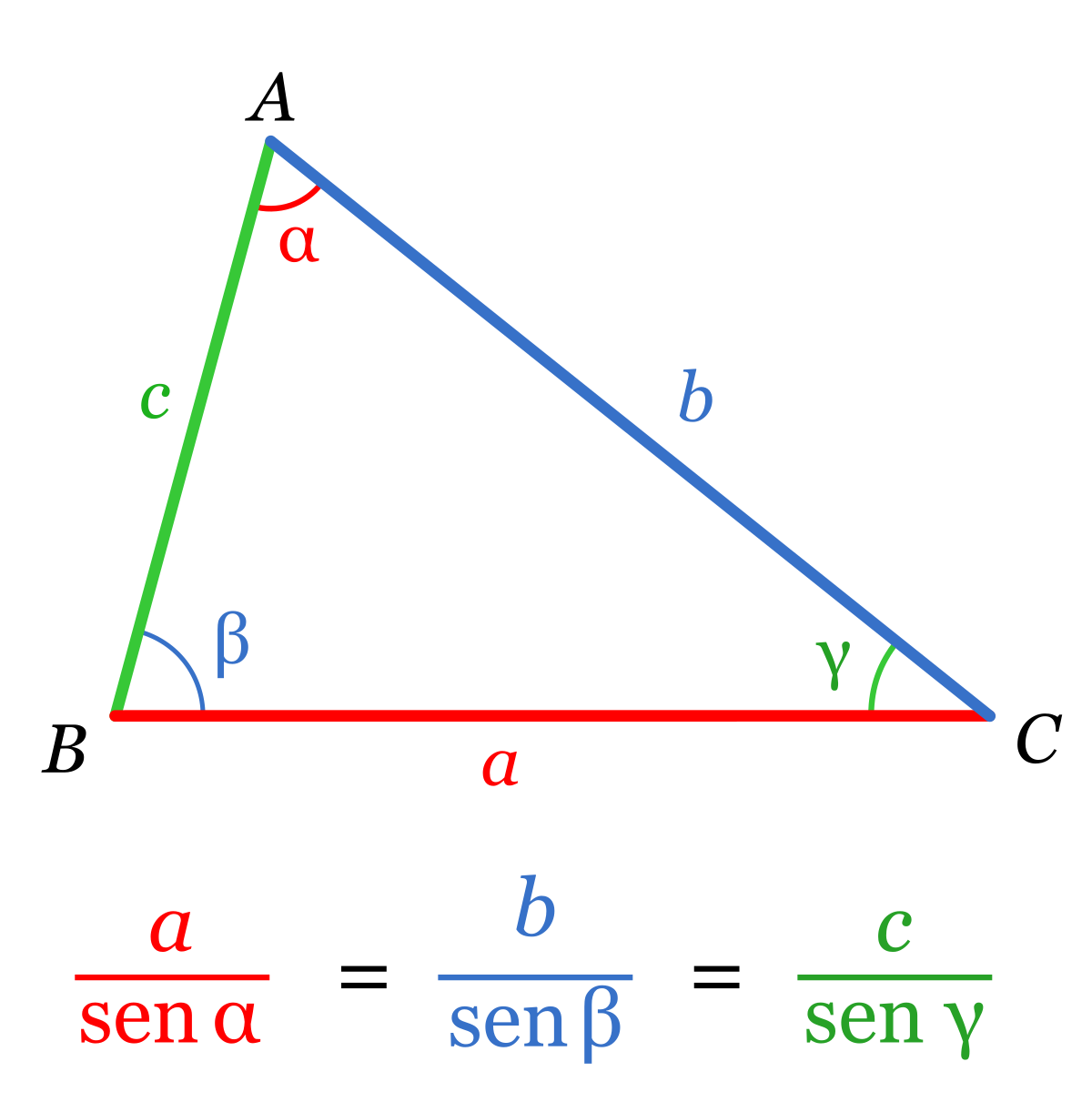
4.-Tanto el teorema del seno como el del coseno son resultados que se pueden aplicar a cualquier triángulo, es decir, no nos hace falta que el triángulo sea rectángulo, como nos pasaba con el teorema de Pitágoras.
El teorema del seno es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos relativamente opuestos. Dado el triángulo:
El teorema del coseno se puede entender como una generalización del teorema de Pitágoras para triángulos cualesquiera, es decir, si aplicamos el teorema del coseno en un triángulo rectángulo obtenemos el mismo resultado que el teorema de Pitágoras. Nos relaciona la longitud de un lado con las longitudes de los otros y con el coseno del ángulo formado por éstos. Dado el triángulo:

Se obtiene: a^2=b^2+c^2-2·b·c·cosα
Además no privilegia ningún lado, de manera que, realmente, se tienen otras dos igualdades:
b^2=a^2+c^2-2·a·c·cos β
c^2=a^2+b^2-2·a·b·cos γ
5.-Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones.
Las funciones trigonométricas son las funciones establecidas con el fin de aplicar la definición de las razones trigonométricas a todos los números reales y complejos.
Una ecuación trigonométrica es aquella en la que las incógnitas aparecen formando parte de los ángulos de funciones trigonométricas.
Como las incógnitas son ángulos, las soluciones que existan serán infinitas (todos los ángulos mayores de 360º con el que hallemos), pero normalmente nos bastará con dar la solución comprendida entre 0º y 360º. También puede darse la solución en radianes.
Para resolver ecuaciones trigonométricas, debemos sustituir las fórmulas de los ángulos que nos vayan apareciendo.

fuente:http://www.vadenumeros.es/primero/formulas-trigonometricas.htm
6.-A pesar de mi enemistad con la materia y mi ausencia en clase durante una semana,este tema no me ha parecido tan pesado como imaginaba.Ya tenía antecedentes con la trigonometría desde 4º,desde ese catastrófico examen por parejas cuya nota no soy capaz de mencionar.Recordaba esta parte de las matemáticas como una puñalada directa al corazón,pero para mi sorpresa,tan solo ha sido un pequeño corte en la rodilla.Aunque no todo ha sido perfecto,aún puedo quedarme mirando una ecuación trigonométrica durante tres horas y no hallar la solución.Pero en general ha sido un tema que ha despertado un mínimo de curiosidad en mi ser.Incluso me ENTRETUVO leer y recordar un poco los 4 primeros apartados de esta entrada mientras la hacía.
Conclusión:mi tolerancia hacia las mates ha aumentado(un poco).